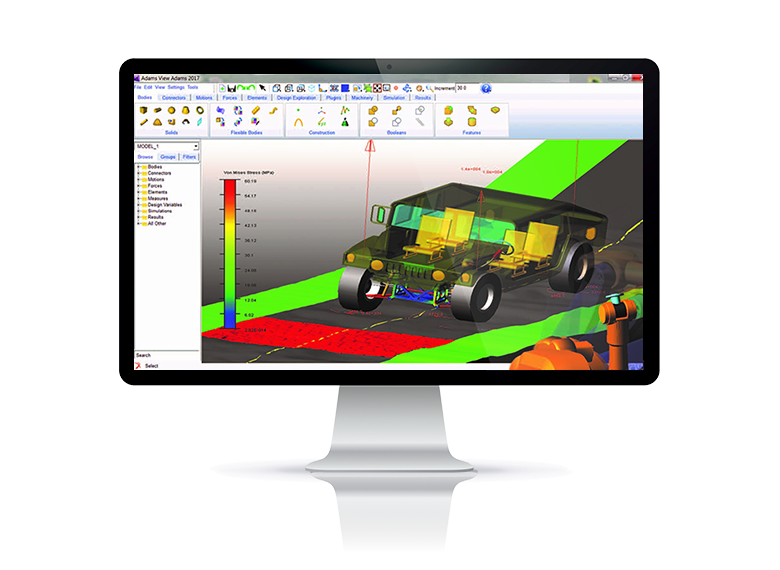
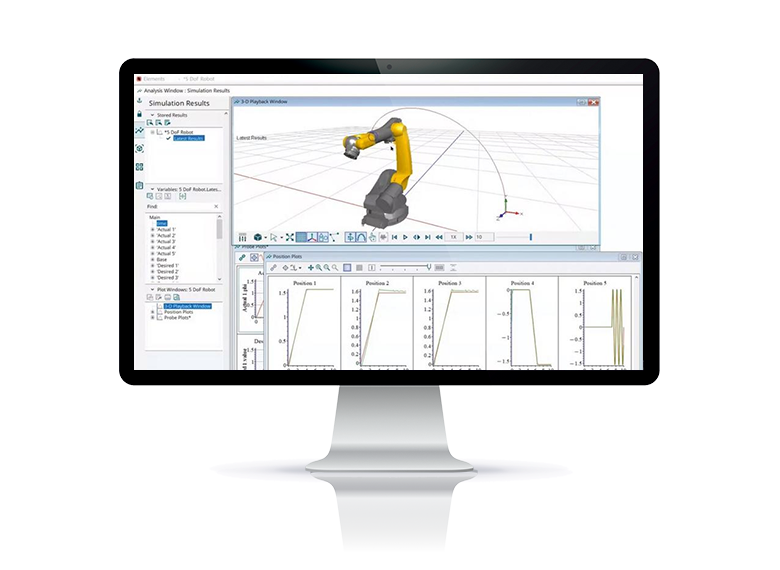
在航空航天領域,對飛行器的姿態需要實時準確的獲取,以便給自控係統或其它相關(guan) 係統傳(chuan) 遞必要基礎數據完成相關(guan) 功能,但是,由於(yu) 飛行器在三維空間中任意姿態飛行,相對全局坐標係進行測量往往達不到理想效果,另外,雖然實現這種測量的手段還有其它,但是往往會(hui) 造成所測角度超過90度會(hui) 產(chan) 生突變,比如彈體(ti) 連續翻滾,因此,有必要采用一種更有效的測量手段應用於(yu) 實際工程中。
本方案的核心在於(yu) 自定義(yi) 約束和AO函數的綜合使用,基於(yu) 創建的虛質量點與(yu) 飛行器測點,相對飛行器指定的局部坐標係進行各軸角度的測量。
虛質量點這裏用點質量模擬,其質量可以設置為(wei) 任意值,因為(wei) ,其質量並不會(hui) 作用到飛行器上。自定義(yi) 約束是Adams為(wei) 了拓展應用靈活性所釋放的一種接口,通過自定義(yi) 函數實現對位移、速度等的約束,滿足工程師比較特殊的需求。AO函數,即Action Only函數,該函數的核心在於(yu) 可以截斷指定對象的約束反力,可以基於(yu) 拉格朗日方程中的拉格朗日乘子進行解釋。
Action only函數在約束方程中具備隔離標量表達式某些部分與(yu) 約束反力的功能。通過對受約束係統的拉格朗日方程進行研究,可以很好地理解Action only函數的作用。
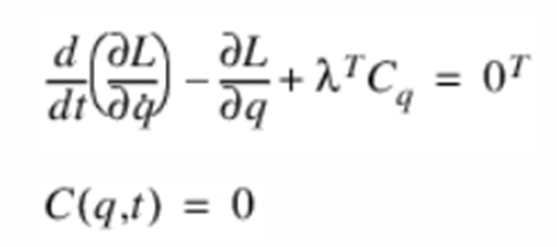
其中,
L為(wei) 係統能量;
Q為(wei) 廣義(yi) 坐標;
C為(wei) 約束;
λ為(wei) 拉格朗日乘子;
通過拉格朗日方程可知,基於(yu) 約束雅可比矩陣將約束反力投影到廣義(yi) 運動方程中,而基於(yu) Action only函數的機製,可以使某些選定的廣義(yi) 坐標免受約束反力的作用,從(cong) 而實現數學上的隔離。
該函數隻能用於(yu) 約束方程表達式中,其形式很簡單AO(exp),這裏的表達式就標明了哪些量將同約束反力隔離。
比如下麵的示例:
描述Marker_1和Marker_2之間的約束方程如下所示:
GCON/1, FUN=DX(1) - AO(DX(2))
GCON/2, FUN=DY(1) - AO(DY(2))
GCON/3, FUN=DZ(1) - AO(DZ(2))
通過上述三條約束方程,實現兩(liang) 個(ge) 點的平動位移綁定,如果不用AO函數,將實現同球鉸一樣的效果,但是這裏使用了AO函數,表現出的效果為(wei) ,約束反力僅(jin) 會(hui) 作用到Marker_1上,而不會(hui) 作用到Marker_2上,從(cong) 作用效果上看,就是實現了將Marker_1推向Marker_2,而不會(hui) 有將Marker_2推向Marker_1的效果。
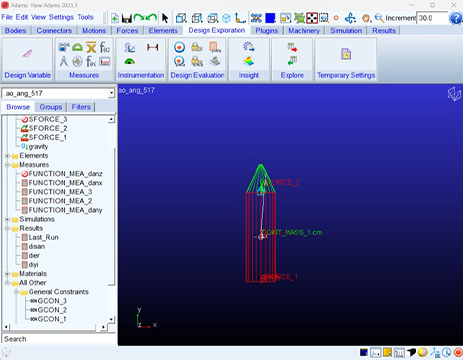
由於(yu) AO函數截斷了虛質量和飛行器之間的相互作用力傳(chuan) 遞,所以其質量不會(hui) 影響飛行器的各種受力,相當於(yu) 虛質量不存在。此時,虛質量僅(jin) 僅(jin) 用於(yu) 角度測量,但是,由於(yu) 自定義(yi) 約束的存在,又能保證虛質量可以同飛行器測點保持同步,這種看似完全不符合力學常識的行為(wei) ,真實發生在了模型上。換句話說,這種方法是基於(yu) 數學的方式解決(jue) 了力學的問題,為(wei) 實際工作提供了便宜。
基於(yu) AO函數和自定義(yi) 約束完成前期準備工作,即可完成後繼的有效測量。
該方法適用於(yu) 飛行器任意狀態下的姿態角獲取,不會(hui) 因為(wei) 多個(ge) 自由度的耦合產(chan) 生相互影響。
由於(yu) AO函數的截斷作用,輔助測量元素和真實係統元素之間沒有力學傳(chuan) 遞作用,不會(hui) 對係統的受力產(chan) 生影響。
完善信息後我們(men) 將會(hui) 盡快與(yu) 您取得聯係,並將資料發送至您的郵箱。感謝您對华体汇官方网站的支持。